A matemática financeira tem como um dos seus principais elementos os juros simples e compostos. Neste resumo, você vai conferir as características de cada um, como eles podem auxiliar na educação dos estudantes e qual é a sua frequência nas provas do ENEM. Logo, prossiga com a leitura para descobrir.
O que são os juros simples e compostos?
Primeiramente, o juro é o rendimento ao credor obtido pelo empréstimo de dinheiro após um período determinado. Essa taxa incide sobre valores conhecidos aos participantes da transação e são geralmente negociadas entre as partes.
Existem dois tipos de juros: o simples e o composto. A seguir, você conhecerá as características, os cálculos e as diferenças desses dois elementos. Contudo, ressaltamos a importância de que as unidades de medidas das fórmulas devem ser correspondentes (por exemplo: dias, meses ou anos). Assim, a taxa de juros e o período determinado estarão sob a mesma conta.
Juros simples
Essa modalidade é uma taxa estabelecida com antecedência sobre o valor primário de um ativo financeiro. Em suma, o juro simples é representado por esta fórmula:
J (juro) = C (capital inicial) x I (taxa de juros) x T (tempo de aplicação).
M (montante final): J + C
Agora, vejamos um exemplo hipotético para uma melhor compreensão. Antônio aplicou R$1.000 em um ativo de juro simples com índice de 10%. Logo, ele terá o rendimento mensal de R$100. Depois de doze meses (um ano), o montante final investido será de R$1.000 + R$1.200, ou seja, R$2.200.
Juros compostos
Por outro lado, os juros compostos funcionam de forma diferente, a partir de uma lógica exponencial de escalonamento. Assim, ele é uma taxa que incide sobre o valor variável de um ativo financeiro. A saber, ele também tem a alcunha de “juros sobre juros” e tem como base a seguinte fórmula:
M (montante) = C (capital) x (1 + I (taxa de juros))n (tempo de aplicação)
Prossigamos com o exemplo do Antônio, mas agora com juros compostos. Os atributos permanecem os mesmos: investimento inicial de R$1.000, com juro de 10% e montante de R$1.100 após um mês.
Entretanto, como o índice é composto, faz-se o cálculo de forma diferente. Em vez de o juro ser aplicado sobre o valor inicial investido, ele deverá incidir sobre o montante acumulado, ou seja, nesse caso de R$1.100 (após um mês). Dessa forma, a taxa de 10% retornará um valor de R$110 no segundo mês, o que representaria um montante de R$1.210 nesse período. Após doze meses (um ano), o total acumulado seria de R$1.000 + R$2.138,43, ou seja, R$3.138,43. Logo, perceba que o valor do rendimento composto é quase o dobro do índice simples.
Ferramenta educacional
Sobretudo, o conhecimento sobre os juros simples e compostos é essencial como ferramenta de educação financeira. Além de ser um conceito matemático importante para a formação escolar, ele também é um princípio elementar de economia que ensinará os alunos a lidarem melhor com o seu dinheiro.
Nesse sentido, os estudantes poderão fazer investimentos mais seguros no futuro, terão mais segurança na obtenção de financiamentos e conseguirão trabalhar de forma competente no mercado financeiro (se assim desejarem).
Frequência no ENEM
Por fim, os juros simples e compostos são um tópico que cai com frequência no Exame Nacional do Ensino Médio. A saber, eles normalmente são abordados em questões que tratam sobre investimentos, pagamentos, compras e parcelamentos, nas quais o candidato deverá selecionar a opção que corresponde ao montante correto. Nesse sentido, veja em quais das últimas edições este assunto foi utilizado:
- 2021;
- 2019;
- 2018;
- 2017;
- 2015;
- 2013;
- 2012;
- 2011;
- 2009.
Exemplo no ENEM
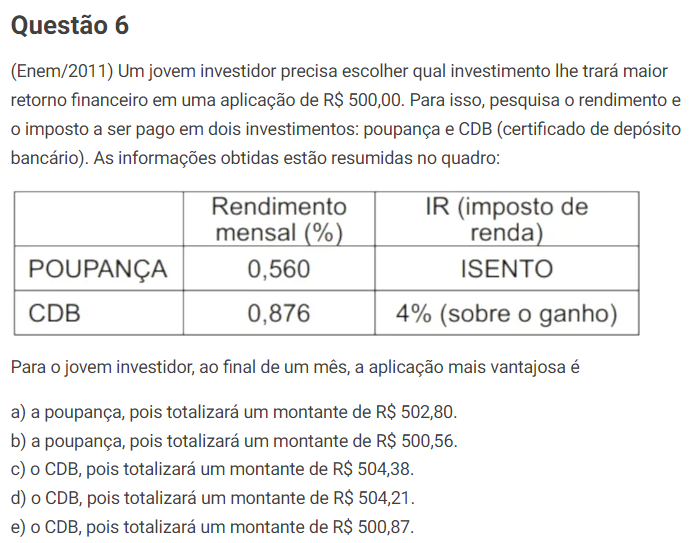
Confira esta questão da prova de 2011:
Resposta: D.
Gostou deste resumo sobre os juros simples e compostos? Então, não deixe de conferir o nosso material sobre média, moda e mediana na seção de matemática.